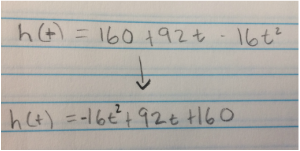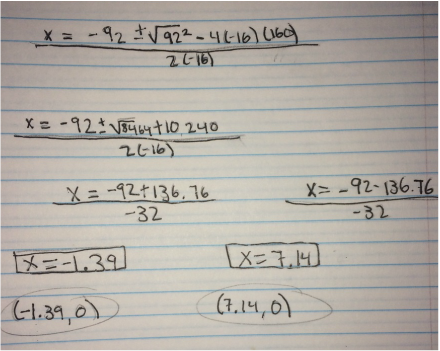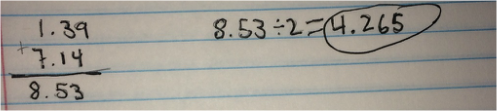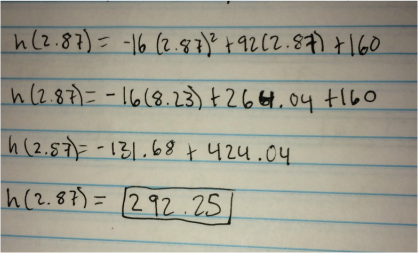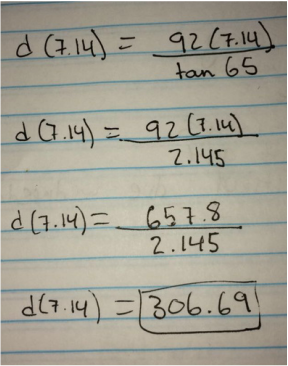Firework Problem

The Problem
In this problem we are tasked to help the director of Jefferson High School with the firework display that will be put on to celebrate their soccer championship. The director wants to ensure the safety of spectators during the show.
We are asked to to draw a diagram that represents the situation, find the fireworks highest point, which is where they will detonate, and where the fireworks will land.
We know that:
We were also given two functions to help us answer this problem
When we first received this problem at the beginning of the semester we did not have the tools we needed to solve this problem such as knowing how to find the special points in a parabola.
Some of the initial questions I had about this problem were:
My first attempts at this problem included blindly and unsuccessfully trying to manipulate the equations and tediously guessing and checking.
In the photo to the right I used the function h(t)=160+92t-16t^2 to try to complete an x,y table. This proved very ineffective because of how time consuming it was. Also, because I was increasing by whole numbers on the x axis it was harder to find the special points when their x coordinate was not a whole number.
Once we were close to completing the quadratics unit, we revisited this problem. The second time around I had a much easier time with this problem because I had the skills to be able to complete it.
Still stuck in my old methods I began working with an x,y table again. Realizing, again, how ineffective it was I drew out the scenario to get a better visual.
In this problem we are tasked to help the director of Jefferson High School with the firework display that will be put on to celebrate their soccer championship. The director wants to ensure the safety of spectators during the show.
We are asked to to draw a diagram that represents the situation, find the fireworks highest point, which is where they will detonate, and where the fireworks will land.
We know that:
- The fireworks are launched from a tower at 160 ft.
- The launcher is at a 65 degree angle from the horizontal
- The initial velocity of the fireworks is 92 ft./sec.
We were also given two functions to help us answer this problem
- h(t)=160+92t-16t^2
- d(t)=92t/tan65
When we first received this problem at the beginning of the semester we did not have the tools we needed to solve this problem such as knowing how to find the special points in a parabola.
Some of the initial questions I had about this problem were:
- How far away do the spectators need to be from the launcher to be safe?
- Where did the debris land?
- How would we find where the debris will land?
- Why is knowing the velocity of the fireworks relevant?
My first attempts at this problem included blindly and unsuccessfully trying to manipulate the equations and tediously guessing and checking.
In the photo to the right I used the function h(t)=160+92t-16t^2 to try to complete an x,y table. This proved very ineffective because of how time consuming it was. Also, because I was increasing by whole numbers on the x axis it was harder to find the special points when their x coordinate was not a whole number.
Once we were close to completing the quadratics unit, we revisited this problem. The second time around I had a much easier time with this problem because I had the skills to be able to complete it.
Still stuck in my old methods I began working with an x,y table again. Realizing, again, how ineffective it was I drew out the scenario to get a better visual.
I then started by trying to find where the fireworks land (the x-intercepts). I did this by taking the the function h(t)=160+92t-16t^2 and applied it to the quadratic formula.
First, I rearranged the function to make it easier to work with.
Next, I input the function into the quadratic formula and solved it. I got the two x intercepts : (-1.39,0) & (7.14,0)
Next I solved for the point where the fireworks will detonate. That point is also the vertex of the parabola. I knew that the vertex is located at the highest and center point of the parabola. So I used information that I already had (the two x intercepts) and made conclusions to help me find the vertex.
I added the two x intercepts to and divided it by two. This gave me 4.26 which represents how many spaces from the x intercept is the center of the parabola. I then used that to find the exact center between the two points: 2.87.
I added the two x intercepts to and divided it by two. This gave me 4.26 which represents how many spaces from the x intercept is the center of the parabola. I then used that to find the exact center between the two points: 2.87.
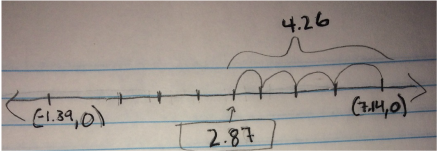
This gave me the x coordinate of the vertex: (2.87,y). I then plugged in the x coordinate into the height function to find the y coordinate of the vertex.
The highest point that the fireworks will reach is: (2.87, 292.25)
Lastly I had to find the distance that the fireworks will travel because although I found the x intercepts, the x axis represents time not distance.
To do this I used the distance functions that was given to us, d(t)=92t/tan65 and plugged in the positive x intercept.
Lastly I had to find the distance that the fireworks will travel because although I found the x intercepts, the x axis represents time not distance.
To do this I used the distance functions that was given to us, d(t)=92t/tan65 and plugged in the positive x intercept.
The farthest distance the fireworks will travel is: 306.69 ft.
Problem Evaluation
I really enjoyed this problem and the quadratics unit. I think it was one of the harder units I’ve had and I really liked how it pushed my thinking by relating what we were learning to some real world problems. I also liked how in this unit every concept that we learned was relevant to each other and built off each other. I also liked how necessary group work was throughout this unit because it helped me grow as a group member.
Self Evaluation
For this unit I think I should receive an A because I worked really hard to keep up with my work and understand all the concepts. I studied very hard to be able to understand and apply the concepts for the tests and I think that was reflected in my results. I also think I worked pretty well as a group member. Even though sometimes I moved a bit quickly when the rest of my group wasn’t there yet I did spend a lot of time explaining to peers and helping others understand the concepts.
Edits
- Finish adding photos
- Format on DP
- Make clarifications on problem evaluation