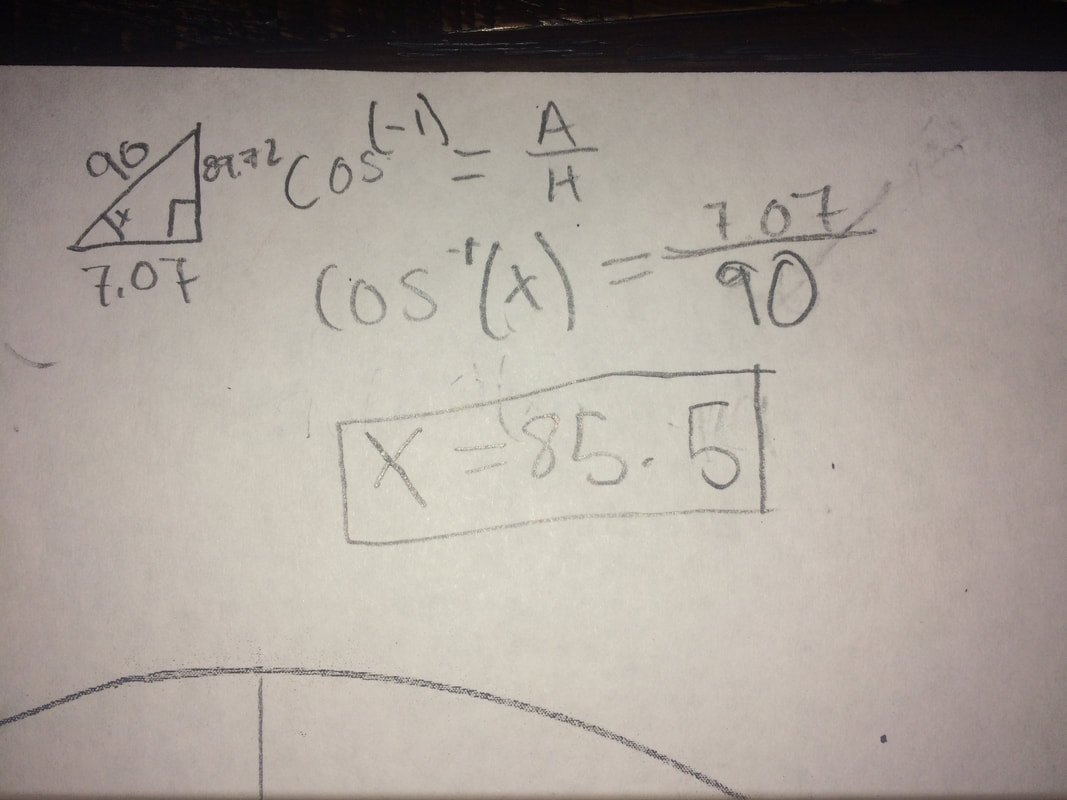Project Statement
The Cow Problem was our unit problem to learn about geometry and trigonometry concepts like Sine, Cosine, Tangent, and the Pythagorean Theorem. In this problem there is a cow that is tied to a 10x10ft barn. The rope that ties the cow to the barn is 100 ft long. We are asked to to find the land area that the cow can graze from, not including the barn. Although it may sound quite simple, once we began visualizing the figure we realized there was more to this problem than we thought.
Process
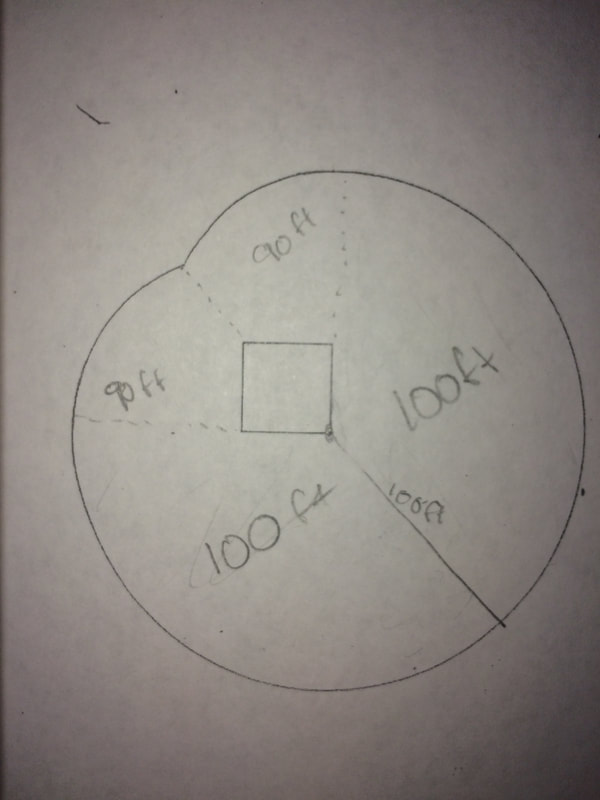
The challenge of visualizing the problem was that, despite what my initial thought was, the shape of the area is not a perfect circle. Only later did I realize, the radius of the circle changes at different points because the cow has to go around the barn. Below are some of my initial attempts of sketching the problem.
As you can see in my final sketches below, about 3/4 of the grazing area was a circle with the rope length (radius) of 100 feet. Then, once the cow passes the first side of the barn, the rope tightens around the barn causing its length to shorten to 90 feet. This creates the two mirrored portions of a circle at the top with a radius of 90 feet.
Once we had manageable shapes, it was time to begin calculating the area of each section.
To calculate the area I needed to:
To calculate the area I needed to:
- Find he dimensions of the triangle - Base, Height & Angles
- Find the angle of the section of circle with the 90 foot radius
- Practice using the Pythagorean Theorem, Sine, Cosine, and Tangent
The only dimensions I had at this point was the outer side that was 90 feet. To find the area you multiply the Base x Height x 0.5 . I still needed the Base and Height. The base was a line that divided the barn, luckily I knew the dimensions of the barn and found that missing side using the Pythagorean Theorem, A^2 + B^2 = C^2. Below is how I solved this equation.
The base I found was 14.14 feet but since I had divided the triangle into two, both had a base of 7.07 feet. Next I had to find the height of the triangle. Again I used the Pythagorean Theorem. The height is 89.72 feet.
|
Now the only sections I had left to find the area of were the two sections of a 90 foot radius circle. I needed to find the angle of the section so I started by finding one the angles of the triangle. I used Cosine and found the angle was 85.5 degrees. I was also able to make the assumption that because the other angle was of half a square, it was 45 degrees.
|
Next I added the two angles I knew and subtracted it from 180, the total degrees in a straight line, to find the missing angle. The angle was 49.5 degrees.
I found the area of the two sections by equation to find an area of a circle but multiplied it by 49.5/360 . I did this because the section was only 49.5 degrees out of the total 360 in a circle. Each section had an area of 3,498.94 feet sq.
Finally I had all of the area of every section to add and find the area.
Lastly, I subtracted the area of the barn that intersected with the triangle sections.
My final answer: the cow's grazing area is 31,144.14 ft square
My final answer: the cow's grazing area is 31,144.14 ft square
Reflection
I really liked working on the cow problem. The part I learned the most from was the practices we had to do to prepare for the problems. A lot of times when I didn't understand, I had to pull my own resources in trying to figure it out. I used Khan Academy outside of class and asked some of my peers to help me understand how to use Sine, Cosine, and Tangent. A section of the cow problem that really pushed my thinking was trying to find the angle of the 90 foot radius section. This was a bit challenging because I had to recall a lot of the geometry unit from last year.
I enjoyed working with my group on the problem and on the group test. Working with people I hadn't before, that had different learning styles and speeds, helped me grow in my cooperative skills. If I were to grade myself I would give myself an A because I was accountable with my work and progress on the problem. I also exemplified my communication skills and understanding of the problem in the way I explained the process to my groupmates that didn't understand. At one point during the group test one of my groupmates was confused as to how we were using the Pythagorean Theorem. Instead of continuing with the problem so I could get to my indivudual test quicker I made sure that everyone stoped and worked together on trying to explain our work to her before we moved on.
I enjoyed working with my group on the problem and on the group test. Working with people I hadn't before, that had different learning styles and speeds, helped me grow in my cooperative skills. If I were to grade myself I would give myself an A because I was accountable with my work and progress on the problem. I also exemplified my communication skills and understanding of the problem in the way I explained the process to my groupmates that didn't understand. At one point during the group test one of my groupmates was confused as to how we were using the Pythagorean Theorem. Instead of continuing with the problem so I could get to my indivudual test quicker I made sure that everyone stoped and worked together on trying to explain our work to her before we moved on.