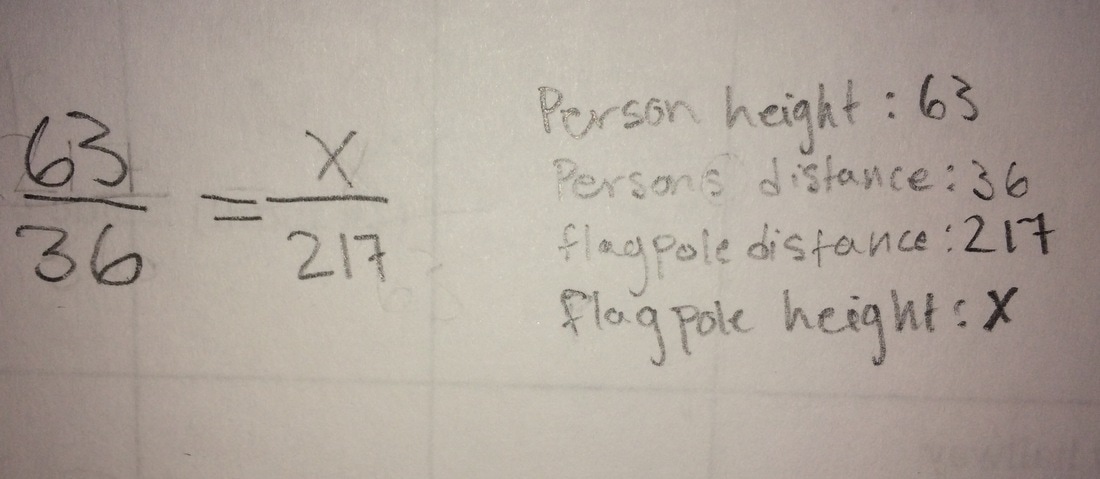Problem Statement
In this unit we used the Flagpole Height Problem to study similarity. Our task was to use 3 different methods to find the height of the school flagpole so we could purchase an appropriate size flag. To solve this problem we learned about similarity through proportions, scale factor, and angles.
Process and Solution
We began this problem by going outside to look at the flagpole and to estimate its height. I tried to compare the flagpole to other objects that had a known height. My initial thought was to estimate how many basketball hoops it would take to reach the height of the flagpole. I knew that a basketball hoop was 10 feet tall so, through estimation, I came to my initial guess of 30 ft.
Similarity is when two shapes are essentially the same shape but in different sizes.
There are a few different theorems we covered in this unit to prove similarity in triangles.
Similarity is when two shapes are essentially the same shape but in different sizes.
There are a few different theorems we covered in this unit to prove similarity in triangles.
- Side-Side-Side Theorem proves similarity when all corresponding sides of the triangles are proportional.
- Angle-Angle Theorem proves similarity when 2 angles in one triangle are equal to its corresponding angles in the other triangle.
- Side-Angle-Side Theorem proves similarity when 2 sides are proportional to its corresponding sides and the angle connecting them are equal.

Shadow method
The shadow method uses the shadow of an object with a known height (a person) to set up a proportion in order to find the unknown height of an object. As you can see in the image to the right, this method creates two triangles.
The shadow method uses the shadow of an object with a known height (a person) to set up a proportion in order to find the unknown height of an object. As you can see in the image to the right, this method creates two triangles.
Before we could set up any proportions we needed to prove similarity between our two triangles. In this method we proved similarity using the Angle-Angle Theorem. In the image beside you can see that both triangles have right angles where the object meets its shadow. Both triangles also have the same angle at the top of its vertical distance because the sun casting the shadows is hitting the objects at the same angle.
Once proving similarity, we could then begin our measurements. We used my group mate, Mia, as our known value. She is 63 in. tall and her shadow was 100 in. long. The shadow of the flagpole was 480 in. long. Next I set up a proportion placing values with their corresponding sides and cross multiplied to find the value of x.
My estimation for the flagpole height using the shadow method was 25.25 ft.
My estimation for the flagpole height using the shadow method was 25.25 ft.
Mirror Method
In the Mirror Method we used two similar triangles made using an object with a known height and a mirror. As you can see in the picture below, we positioned a mirror in between a person and the flagpole so that the person could see the top of the flagpole. This created two triangles that we could create a proportion for.
Again, to set up a proportion we needed to prove similarity first. We proved similarity through the Angle-Angle Theorem. Both triangles had equal right angles and because of the principle of light reflection, we know the angles reflecting from the mirror were equal.
The proportion we set up for this method looked like this:
|
Each variable represents one side of the triangles. AB represents the person’s height and AC represents the distance from the person to the mirror. XC represents the distance from the flagpole to the mirror and XY is the unknown height of the flagpole.
Lastly, we replaced the variables with the measurements we collected and cross multiplied to get find X. |
My estimate for the flagpole height, using the mirror method was 31.7 ft.
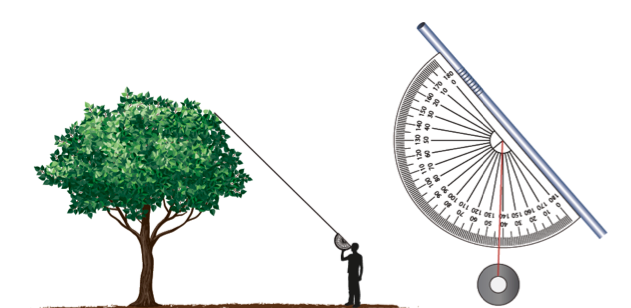
An isosceles is a triangle with two equal sides and angles. The clinometer method creates an isosceles triangle so by finding the length of one of the equal sides, we can find the height of the flagpole.
To find the length of one of the sides we added the height of the person with the distance of the person to the flagpole.
To find the length of one of the sides we added the height of the person with the distance of the person to the flagpole.
My estimation for the flagpole height using the clinometer method was 31.25 ft.
My Final Estimation
My final estimation for the height of the flagpole is 31 ft. I think it is 31 ft. because throughout the 3 methods we used, I calculated 31 ft. 2/3 times.
Problem Evaluation
I enjoyed this problem because working with angles came easily to me. I also liked that I had to use logic to prove similarity using the theorems we learned. Completing this write up pushed my thinking because I had to tie together everything I have done so far in this unit especially all the sub-topics we learned.
Self Evaluation
I would grade myself an A+ in this unit because I was on top of my work and completed it on time. I used my work time in class wisely and I put in time after school to complete assignments like the rubric questions. I worked well with my group and actively participated in out group discussions. I understood the content of the unit well enough help guide others through problems and do minimal revisions on my test.
Edits
- Crop picture
- Add values on triangle
- Add final estimation
- Change photo positioning